Práctica Computacional: La Ecuación de Schrödinger
Oscilador Armónico

Instructor: Darío Mitnik


Parte teórica

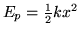Resolver el estádo básico (ground state) del oscilador armónico, $E_p = \frac{1}{2}kx^2$. 


Procedimiento de solucion: probar la posible solucion
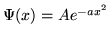$\Psi(x) = Ae^{-ax^2}$, 
donde A y a son constantes, que se determinaran reemplazando esta funcion 
en la Ecuacion de Schrodinger. 

Si bien este problema admite solucion general (para todos los niveles), 
esta es demasiado engorrosa para el presente curso. 
En la derivacion, tener en cuenta que al reemplazar la funcion dada, 
los coeficientes de las distintas potencias deben cancelarse individualmente.

Preguntas

  1. Cuál es la energía del estado básico?
  2. Cuál es la paridad de esta funcion de onda?
  3. Calcular 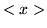$<x>$ y $<x^2>$
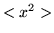
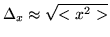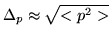  4. suponiendo que $\Delta_x \approx \sqrt{<x^2>}$, y $\Delta_p \approx \sqrt{<p^2>}$, expresar 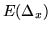$E(\Delta_x)$. Usando el principio de incertidumbre y calculando el mínimo de 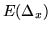$E(\Delta_x)$, estimar la energía del estado básico.
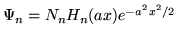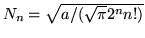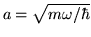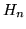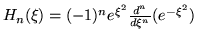  5. La solución general del problema es: $\Psi_n = N_n H_n(ax) e^{-a^2x^2/2}$, donde $N_n=\sqrt{a/(\sqrt{\pi}2^n n!)}$ y $a=\sqrt{m\omega/\hbar}$, y $H_n$ son los polinomios Hermite: $H_n(\xi) = (-1)^n e^{\xi^2}\frac{d^n}{d\xi^n}(e^{-\xi^2})$.

Parte computacional

El ejemplo OSCILLATOR.NB puede ser utilizado en el programa MATHEMATICA, para resolver los siguientes ejercicios:

  1. Graficar las 4 primeras funciones de onda.
  2. Cuál es la paridad de las funciones de onda?
  3. Graficar las densidades de probabilidad.
  4. Comparar descriptivamente estas soluciones con el caso clásico.

oscillator.nb 


[Graphics:Images/oscillator.nb_gr_1.gif]
[Graphics:Images/oscillator.nb_gr_2.gif]

[Graphics:Images/oscillator.nb_gr_3.gif]

[Graphics:Images/oscillator.nb_gr_4.gif]

[Graphics:Images/oscillator.nb_gr_5.gif]


Darío Mitnik
U.B.A.